Units in CMB physics

AST9240 - The Microwave Sky

MJy/sr

普朗克定律（Planck’s Law）

\[ B_{\nu}=\frac{2h\nu^3}{c^2}\frac{1}{\mathrm{exp}(h{\nu}/kT)-1} \]

\(B_\nu\) 的单位是\(\mathrm{erg/s/sr/m^2/Hz}\) ，但是在CMB物理中我们通常用的单位是Jansky，是\(B_\nu\)对立体角 \(\Omega\) 的积分

\[ \mathrm{1\ Jy=10^{-23}\ erg/s/m^2/Hz} \]

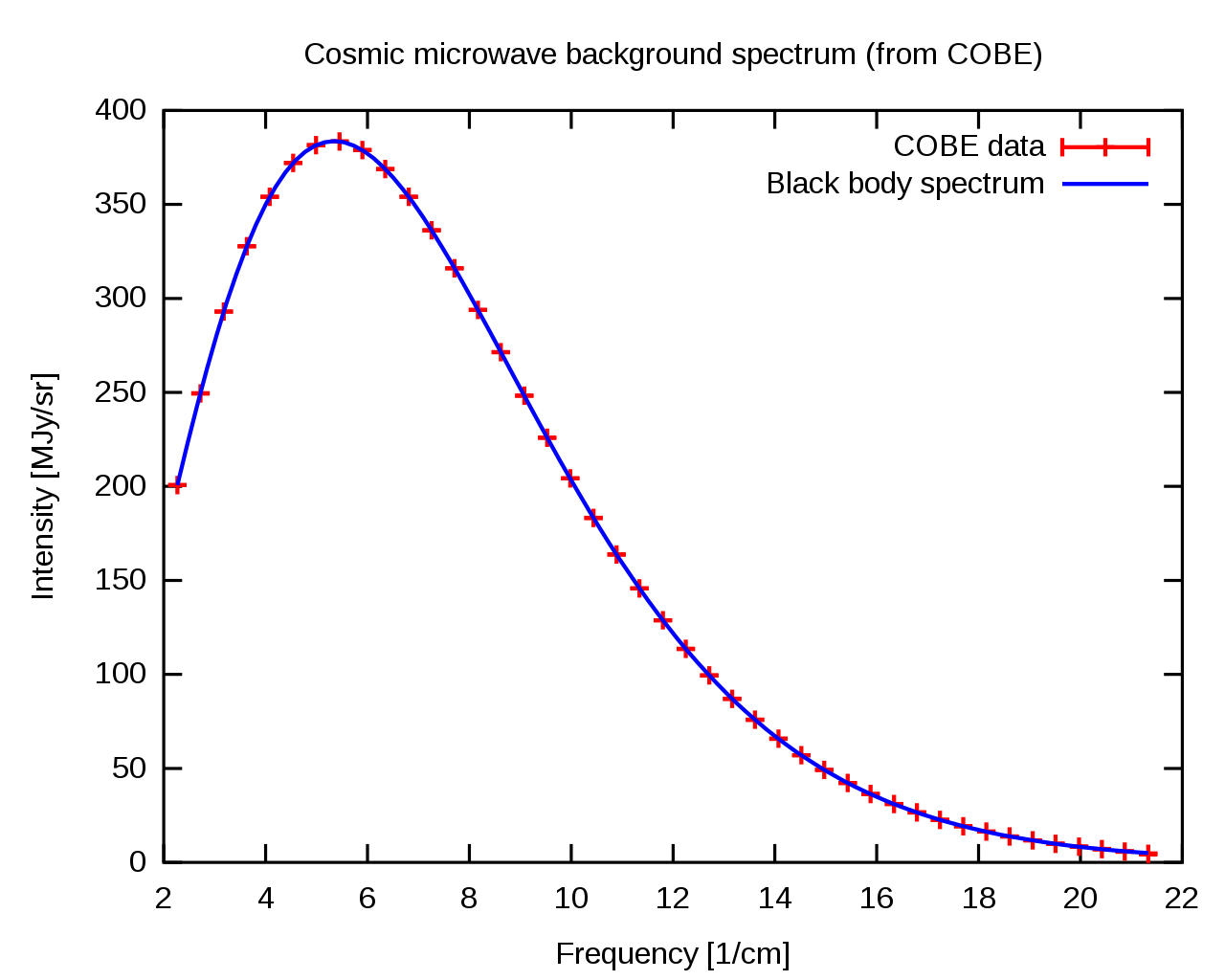
上面图中，电磁波的频率单位换算是这样的

\[ f\mathrm{[GHz]} = 30\times f\mathrm{[cm^{-1}]} \]

\(\mathrm{KJy/sr}\) 是前景分析中经常用到的单位。

K_RJ

瑞利-金斯定律（Rayleigh-Jeans Law）是黑体辐射的低频近似

\[ B_\nu\approx\frac{2\nu^2 kT}{c^2} \]

由这个近似我们可以定义瑞利-金斯温度（Rayleigh-Jeans Temperature）

\[ T_\mathrm{RJ}\equiv\frac{I_\nu c^2}{2\nu^2 k} \]

这样温度和辐射强度是一个简单的线性关系，给定一个天空中某一位置的辐射 \(I_\nu\)，我们就可以的到它的温度，\(\mathrm{K_{RJ}}\) 是在前景分析中经常用到的单位，在分析低频尘埃辐射的时候非常方便。

K_CMB

在实际做观测的时候，显然我们不可能对天空中每一个位置都测一遍黑体谱然后根据拟合确定它的温度。测量一个给定带宽下的全天辐射是效率更高的，类似于天文学里测光的概念，只不过在测光中我们最终想要的到的量是星等，在CMB测量中我们想要的量是温度。

这就需要找到 \(\Delta I_\nu \) 和 \( \Delta T_\mathrm{CMB} \) 之间的对应关系，因为扰动在 \( 10^{-5} \) 量级，只考虑到一阶

\[ \Delta I_\nu=\left(\frac{\partial B_\nu}{\partial T}\right)_{T_\mathrm{CMB}}\Delta T =\frac{2h\nu^3}{c^2}\frac{xe^x}{(e^x-1)^2}\frac{\Delta T_\mathrm{CMB}}{T_\mathrm{CMB}} \]

其中 \(x=h\nu/kT_\mathrm{CMB}\)，这个单位的好处是所有频段都将的到同样的温度扰动 \( \Delta T_\mathrm{CMB} \)，但是因为 \(e^x\) 的存在，不适合高频CMB前景的分析。

K_CMB to K_RJ

\[\begin{aligned} \Delta T_\mathrm{RJ}&=\frac{\Delta I_\nu c^2}{2\nu^2k} = \frac{2h\nu^3}{c^2}\frac{xe^x}{(e^x-1)^2}\frac{\Delta T_\mathrm{CMB}}{T_\mathrm{CMB}}\frac{c^2}{2\nu^2k}\\ &= \frac{h\nu}{kT_\mathrm{CMB}}\frac{xe^x}{(e^x-1)^2}\Delta T_\mathrm{CMB} \\ &=\frac{x^2e^x}{(e^x-1)^2}\Delta T_\mathrm{CMB} \end{aligned}\]

# Constants
kB     = 1.38e-23      # Boltzmanns constant
Tcmb   = 2.7255        # CMB temperature
h      = 6.626e-34     # Plancks constant

# Unit conversion between Rayleigh–Jeans units and cmb units
def Kcmb_to_Krj(nu):
    # nu in GHz
    x = h * nu * 1.0e9 / (kB * Tcmb)
    return x**2 * np.exp(x) / (np.exp(x) - 1.)**2