Spin-weighted Spherical Harmonics
参考 Grant Salton 论文 第二章和 Zaldarriaga & Seljak 1997 的文章。因为斯托克斯参量中的 Q 和 U 场是依赖坐标系定义,普通的球谐变换处理之后的到的物理量也是依赖坐标系的,但是我们需要的物理量最好是不随坐标系变化的,所以需要引入特殊的球谐函数。
Spin
Definition: A spin-s function \(_sf(\theta, \phi)\) is one that, under a rotation of \((\bm{e}_1, \bm{e}_2)\) by an angle \(\psi\) about \(\bm{n}\), transforms via
\[_sf\rightarrow e^{-is\psi}{_s}f \]
Spin Raising and Lowering
We define the spin rasing operator \(\eth\) and spin lowring operator \(\bar{\eth}\)
\[ \eth=-(\sin\theta)^s\left[ \frac{\partial}{\partial\theta}+\frac{i}{\sin\theta}\frac{\partial}{\partial\phi} \right](\sin\theta)^{-s} \]
\[ \bar{\eth}=-(\sin\theta)^{-s}\left[ \frac{\partial}{\partial\theta}-\frac{i}{\sin\theta}\frac{\partial}{\partial\phi} \right](\sin\theta)^s \]
The spin-weighted spherical harmonics are then defined as
\[ _sY_\ell^m=\sqrt{\frac{(\ell-s)!}{(\ell+s)!}}\eth^s Y_\ell^m\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (0\leq s\leq\ell) \]
\[ _sY_\ell^m=\sqrt{\frac{(\ell+s)!}{(\ell-s)!}}(-1)^s\bar{\eth}^{-s} Y_\ell^m\ \ \ \ \ (-\ell\leq s\leq 0) \]
Properties
The spin-weighted harmonics satisfy orthogonality and completeness
\[\int {_s}Y_{\ell}^m(\theta,\phi) \ {_s}Y_{\ell^\prime}^{m^\prime}(\theta,\phi)^*\mathrm{d}\Omega = \delta_{\ell\ell^\prime} \delta_{mm^\prime} \]
\[\sum_{\ell m} {_s}Y_{\ell}^m(\theta,\phi)\ {_s}Y_{\ell}^{m}(\theta^\prime,\phi^\prime)^*=\delta(\cos\theta-\cos\theta^\prime)\delta(\phi-\phi^\prime) \]
Other important properties
\[ \eth {_s}Y_\ell^m=+\sqrt{(\ell-s)(\ell+s+1)}\ {_{s+1}}Y_\ell^m \]
\[ \bar{\eth} {_s}Y_\ell^m=-\sqrt{(\ell+s)(\ell-s+1)}\ {_{s-1}}Y_\ell^m \]
Stokes QU
根据斯托克斯参量的定义
\[\begin{aligned}Q&=Ip\cos2\psi\cos2\chi \\ U&=Ip\sin2\psi\cos2\chi \end{aligned}\]
当我们旋转坐标系的时候,\(\chi\) 并不发生变化,但是 \(\psi\rightarrow\psi+\Delta\),我们得到一组新的斯托克斯参量值
\[\begin{aligned}Q^\prime&=Ip\cos2\psi^\prime\cos2\chi \\ U^\prime&=Ip\sin2\psi^\prime\cos2\chi \end{aligned}\]
我们构造一组量 \(Q\pm iU\),可以证明它们分别是自旋 \(\pm2\) 的量,以 \(Q+iU\) 为例,令 \(Ip=1\)
\[\begin{aligned}Q^\prime+iU^\prime&=\cos2\psi^\prime\cos2\chi+i\sin2\psi^\prime\cos2\chi \\ &=(\cos2\psi\cos2\Delta-\sin2\psi\sin2\Delta)\cos2\chi \\ &\ \ \ \ \ + i(\sin2\psi\cos2\Delta+\cos2\psi\sin2\Delta)\cos2\psi \\ &=Q\cos2\Delta-U\sin2\Delta+i(U\cos2\Delta+Q\sin2\Delta) \\ &=(Q+iU)(\cos2\Delta+i\sin2\Delta) \\ &=(Q+iU)e^{i2\Delta} \end{aligned}\]
E and B modes
把复数标量场 \(Q\pm iU\) 按照自旋为 2 的球谐函数展开
\[(Q\pm iU)(\theta,\phi)=\sum_{\ell m} {_{\pm2}}a_{\ell m}\ {_{\pm2}}Y_\ell^m(\theta,\phi)\]
定义新的量,用来确定偏振的信息
\[\begin{aligned}a_{E,\ell m}&=-\frac{1}{2}({_2}a_{\ell m} + {_{-2}}a_{\ell m}) \\ a_{B,\ell m}&=\frac{i}{2}({_2}a_{\ell m} - {_{-2}}a_{\ell m})\end{aligned}\]
由这两个系数可以定义新的自旋为零的场
\[\begin{aligned} E(\theta,\phi)&=\sum_{\ell m} a_{E,\ell m}\ Y_\ell^m(\theta,\phi) \\ B(\theta,\phi)&=\sum_{\ell m} a_{B,\ell m}\ Y_\ell^m(\theta,\phi) \end{aligned}\]
可以看出 \(EB\) 场和 \(QU\) 场就是简单的导数的关系,通过自旋的升降把 \(Q\pm iU\) 变为零自旋的场
\[\color{black}\begin{aligned}E(\theta,\phi)&=-\frac{1}{2}\Large{[}\normalsize \bar{\eth}^2(Q+iU)+\eth^2(Q-iU) \Large{]}\normalsize\\ B(\theta,\phi)&=\frac{i}{2}\Large{[}\normalsize \bar{\eth}^2(Q+iU)-\eth^2(Q-iU) \Large{]}\end{aligned}\]
出于兴趣,我尝试着画了一下它们的区别:可以明显看到它们之间的区别,\(QU\)有明显的纹路,是依赖坐标系的,而 \(EB\) 呈现的是各向同性的特征。
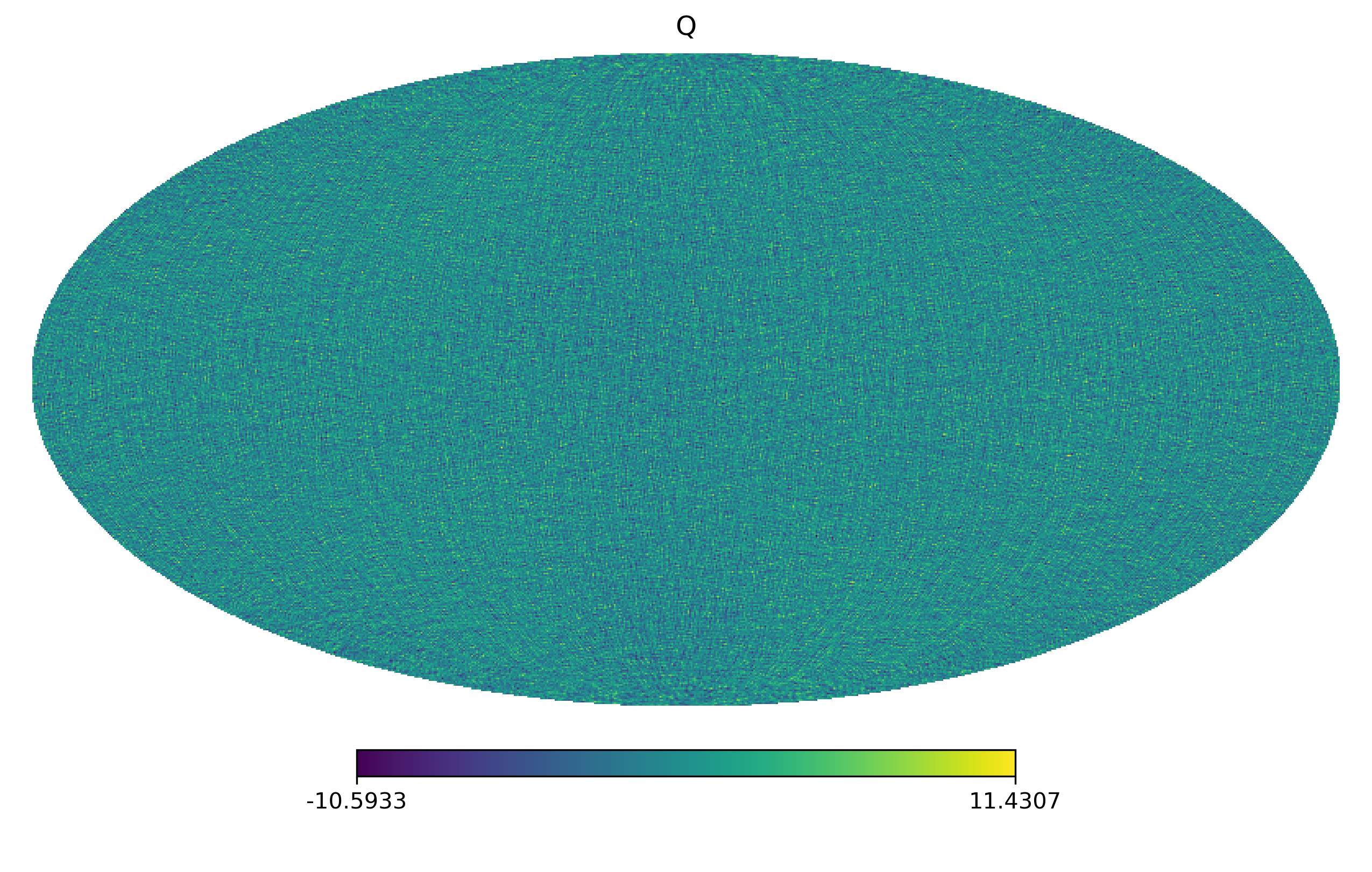
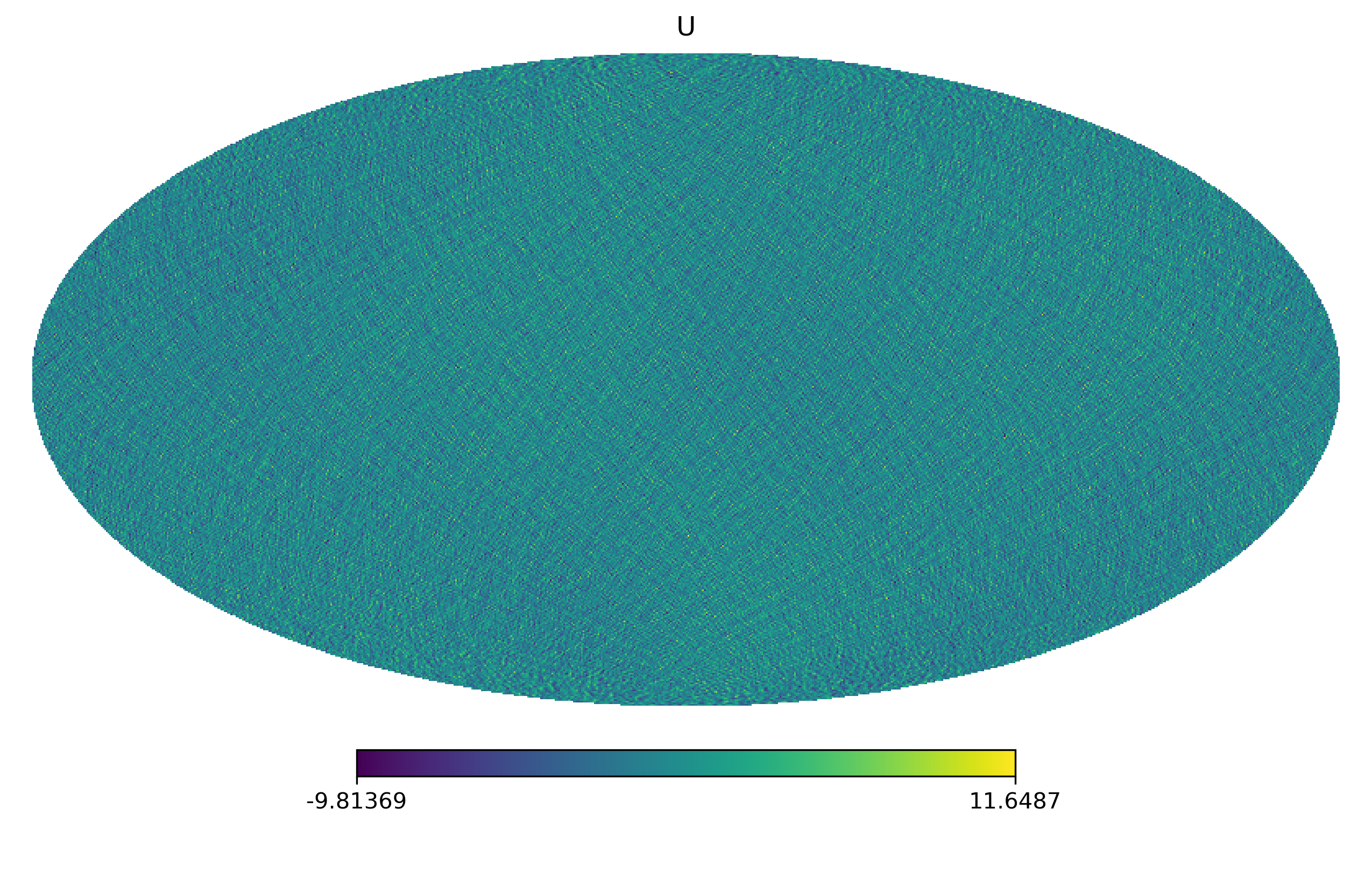
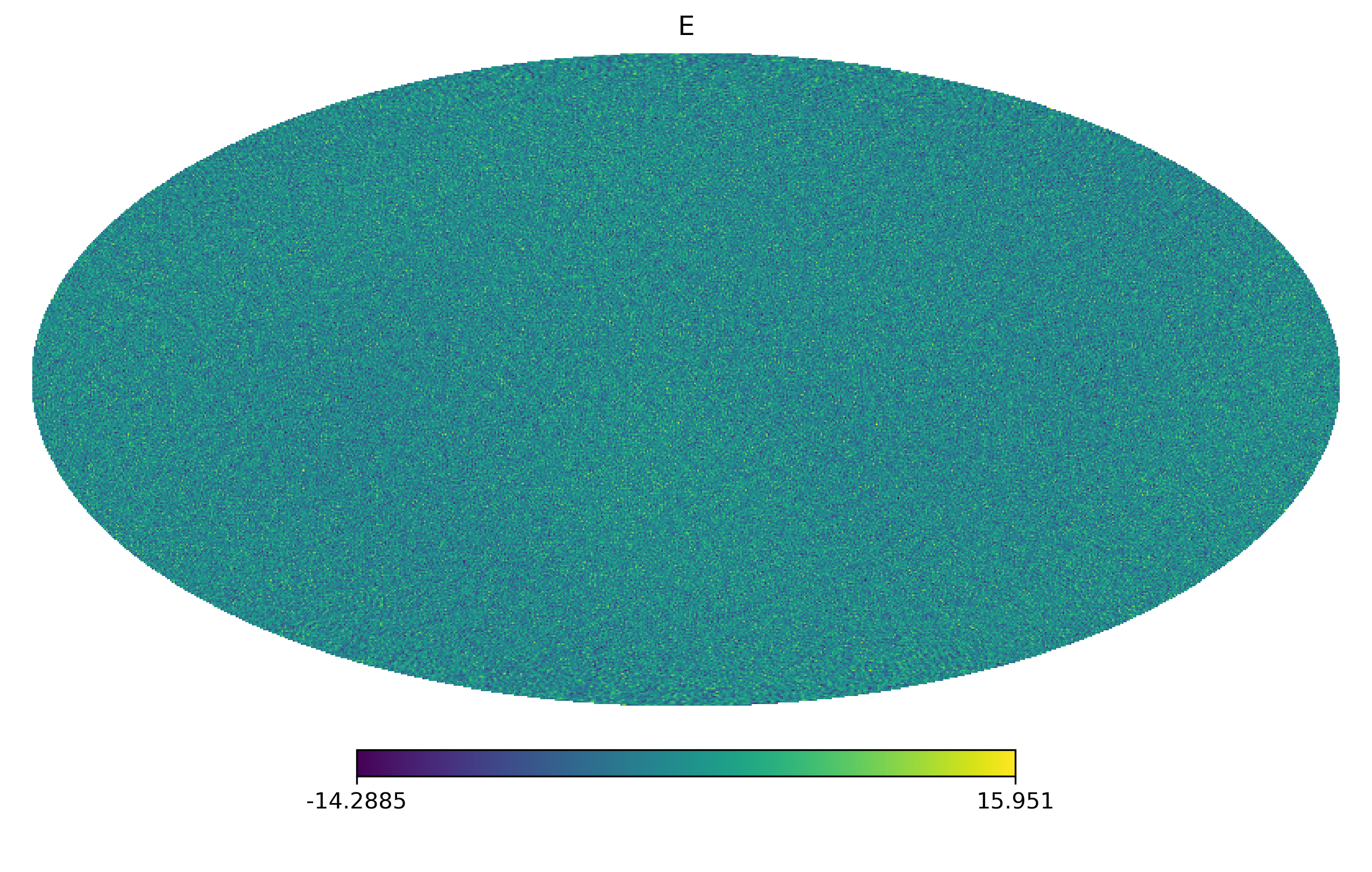
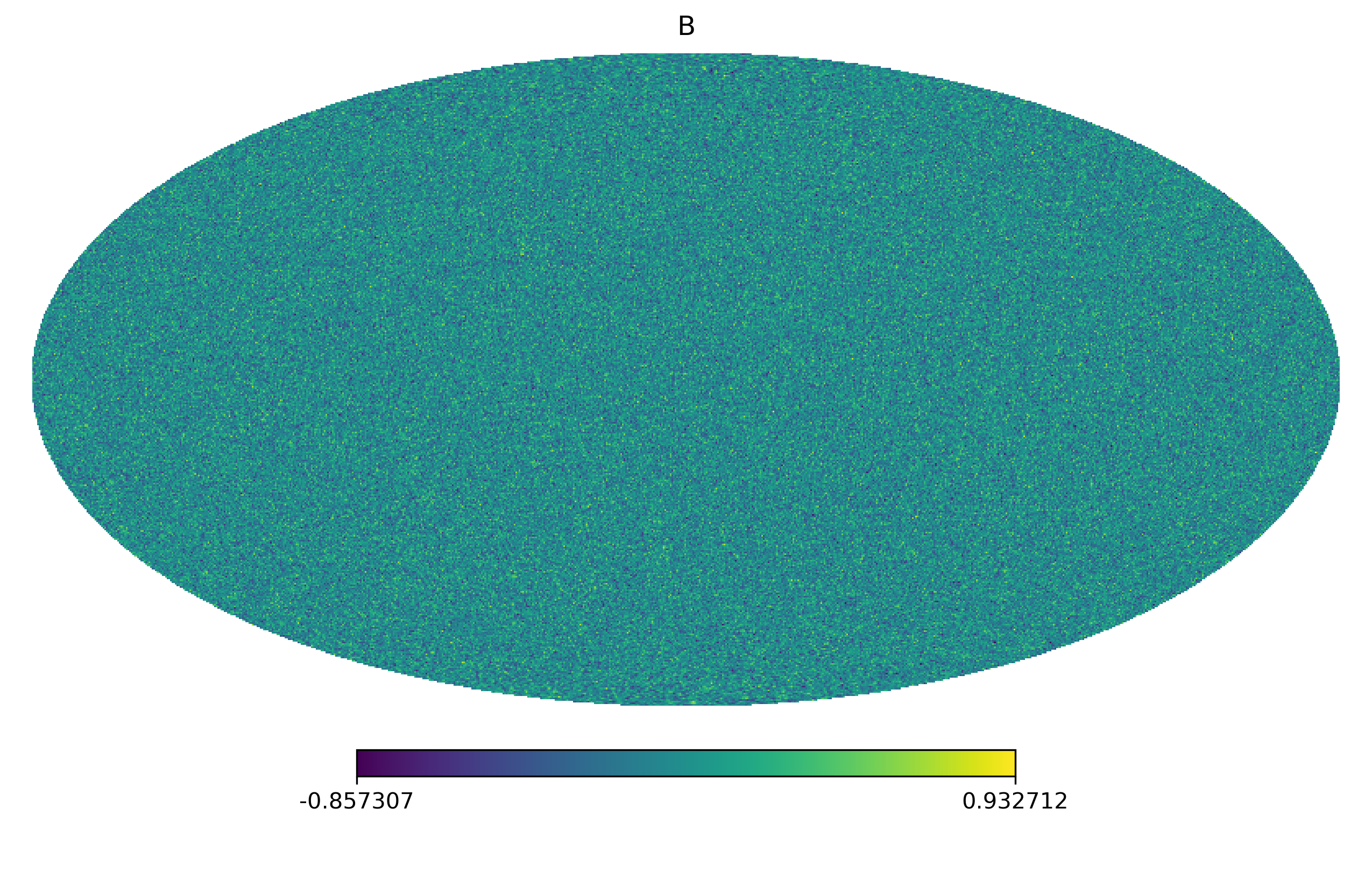
Spin-weighted Spherical Harmonics
https://jinyiliu.github.io/2021/11/19/Spin-weighted-Spherical-Harmonics/