Stokes Parameters
在我学习微波背景辐射的早期,为了预防自己不停地温习斯托克斯参量的定义,写了这篇小记。
EM Radiation
我们通常用电矢量代表电磁波。真空中电磁波的电场方程满足
\[\left( \nabla^2-\frac{1}{c^2}\frac{\partial^2}{\partial t^2} \right)\vec{E}=0 \]
其平面波解为
\[\vec{E}(\vec{r},t)=\vec{E}_0 e^{i(\vec{k}\cdot\vec{r}-\omega t+\varphi)} \]
这是一个数学解,只取实部作为物理解。有时常把常数相位因子 \(e^{i\varphi}\) 并入振幅中,则
\[\vec{E}(\vec{r},t)=\vec{E}_0 e^{i(\vec{k}\cdot\vec{r}-\omega t)} \]
注意,这个时候 \(\vec{E}_0\) 已是复数。
Polarizaiton
为了研究电磁波的偏振态,我们将电矢量分为两个分量
\[ E_x=E_{0x}\cos(kz-\omega t +\varphi_x)\\ E_y=E_{0y}\cos(kz-\omega t +\varphi_y)\]
这是一个用于展示电磁波偏振椭圆的脚本
import numpy as np |
上面所提到的电磁波平面解总是处于线偏振、圆偏振或者椭圆偏振中。在自然界中,电矢量可以朝着任意方向做运动。这些光的相位、偏振方向各不相同,呈现随机分布,所以我们看到的这些辐射的总和是没有特定偏振方向的,这就是自然光。
这里所讨论的都是标量偏振光,还有矢量偏振光,它在横截面上每一点的偏振状态都不一样,并不是均匀分布的。最典型的矢量偏振光是轴对称矢量光,它是 Helmholtz 方程在柱坐标下的特解。
Stokes Parameters
下面是一个偏振椭圆
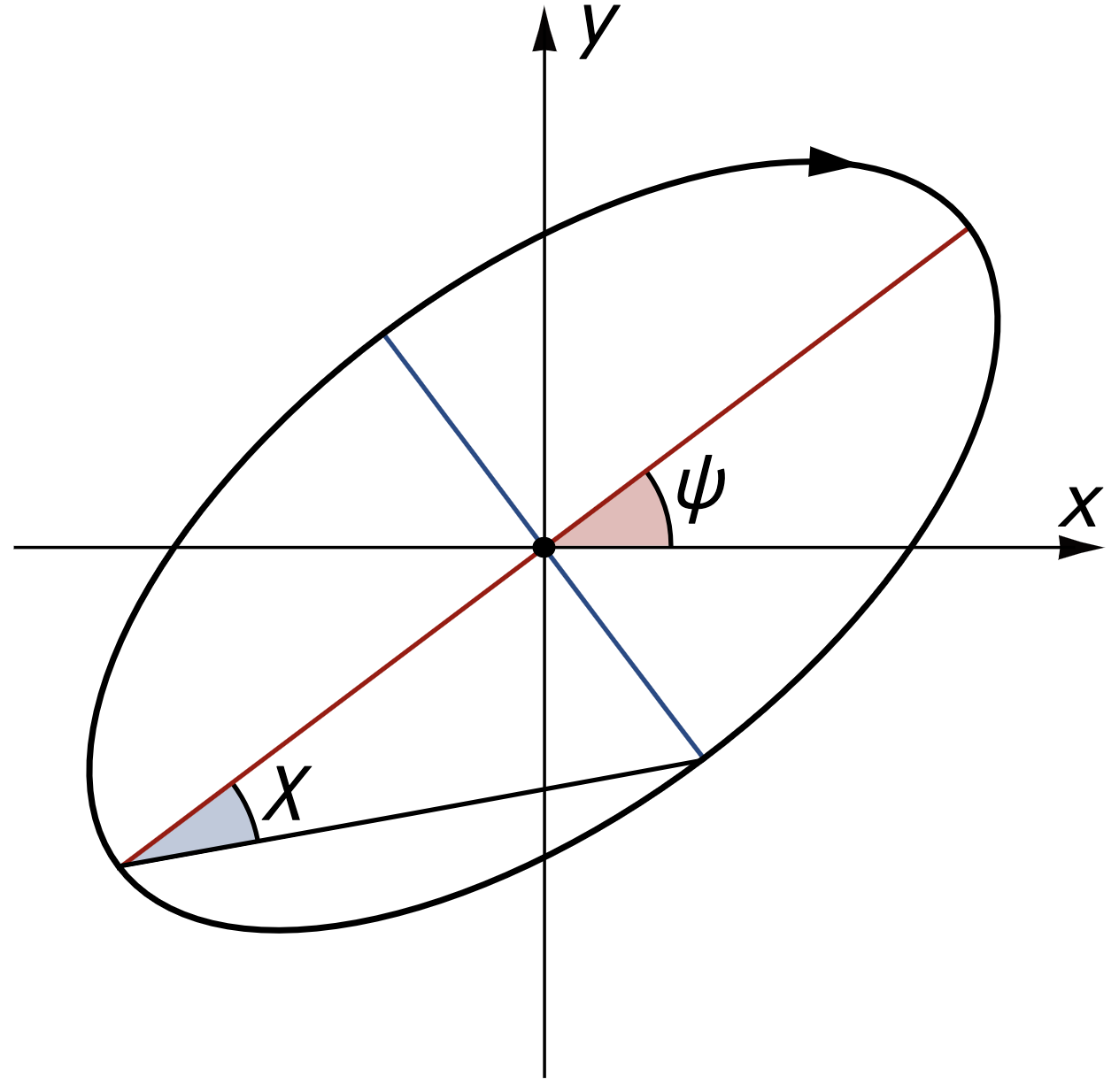
\(\chi=0\) 表示线偏振,反之则表示椭圆偏振或圆偏振,\(\psi\) 表示偏振的方向。斯托克斯参量分别为
\[\begin{aligned}I&=I \\ Q&=Ip\cos2\psi\cos2\chi \\ U&=Ip\sin2\psi\cos2\chi \\ V&=Ip\sin2\chi \end{aligned}\]
其中 \(p\) 表示偏振的程度
\[ p=\frac{\sqrt{Q^2+U^2+V^2}}{I} \]
- \(I\) 正比于入射光的总光强
- \(Q\) 表征了光是更接近于 \(x\) 方向偏振(\(Q>0\))还是 \(y\) 方向偏振(\(Q<0\))
- \(U\) 表征了光是更接近于 \(+45^\circ\) 方向偏振(\(U>0\))还是 \(-45^\circ\) 方向偏振(\(U<0\))
- \(V\) 表征了光是更接近于右旋光偏振(\(V>0\))还是左旋光偏振(\(V<0\))
斯托克斯参量如此定义就是为了测量方便。关于具体如何测量参数的值,可以参考 「知乎」矢量偏振光简介。
Stokes Parameters