Window Functions in CMB experiments

参考 White & Srednicki 1994 和 Page 2003 文章。在微波背景辐射实验中，最重要的一个仪器参数就是仪器分辨率（beam FWHM），它决定了我们是否能够观测到足够小的尺度，这和宇宙参数限制息息相关，同时微波背景辐射透镜效应的重构也依赖小尺度的信号，分辨率足够高，我们的到的重构结果也能够更好。

Window Function

仪器分辨率本质上是一个窗函数的特征尺度，窗函数和真实信号的卷积就是我们观测到的信号，这个过程本质上是一个对真实信号的映射

\[\color{black}\widetilde{T}(\bm{n})=\int\mathrm{d}\Omega_{\bm{n}^\prime}M(\bm{n}, \bm{n}^\prime)T(\bm{n}^\prime) \]

有很多跟仪器相关的效应都可以收入到 mapping function \(M(\bm{n}, \bm{n}^\prime)\) 中，比如 beam 效应。有了 mapping function 就可以计算 window function \(W_\ell(\bm{n}, \bm{n}^\prime)\)

\[\color{black}\langle\widetilde{T}(\bm{n}_1)\widetilde{T}(\bm{n}_2)\rangle=\frac{1}{4\pi}\sum_\ell(2\ell+1)C_\ell W_\ell (\bm{n}_1, \bm{n}_2)\]

其中 window function 的表达式是

\[\color{black}\small\begin{aligned} W_\ell(\bm{n}_1, \bm{n}_2) &= \int\mathrm{d}\Omega_{\bm{n}_1^\prime}\int \mathrm{d}\Omega_{\bm{n}_2^\prime} M(\bm{n}_1, \bm{n}_1^\prime) M(\bm{n}_2, \bm{n}_2^\prime)P_\ell(\bm{n}_1^\prime\cdot \bm{n}_2^\prime) \\ &=\frac{4\pi}{2\ell+1}\sum_m\int\mathrm{d}\Omega_{\bm{n}_1^\prime}\int \mathrm{d}\Omega_{\bm{n}_2^\prime} M(\bm{n}_1, \bm{n}_1^\prime) M(\bm{n}_2, \bm{n}_2^\prime)Y_\ell^m(\bm{n}_1^\prime)Y_\ell^{m*}(\bm{n}_2^\prime)\\ &=\frac{4\pi}{2\ell+1}\sum_m\int\mathrm{d}\Omega_{\bm{n}_1^\prime} M(\bm{n}_1, \bm{n}_1^\prime)Y_\ell^{m*}(\bm{n}_1^\prime)\int \mathrm{d}\Omega_{\bm{n}_2^\prime} M(\bm{n}_2, \bm{n}_2^\prime)Y_\ell^m(\bm{n}_2^\prime) \end{aligned}\]

一般来说，窗函数的映射 \(M(\bm{n}, \bm{n}^\prime)\) 在全天都是一样的，不依赖于 \(\bm n\) ，只依赖于 \(\bm{n}^\prime - \bm{n}\)，也就是上面的积分跟 \(\bm{n}_1\) 和 \(\bm{n}_2\) 无关。所以上面的式子可以简化为

\[\color{black}\begin{aligned} W_\ell(\bm{n}, \bm{n}) &= \frac{4\pi}{2\ell+1}\sum_m\left|M_{\ell m}\right|^2 \end{aligned}\]

之后把 \(W_\ell(\bm{n}, \bm{n})\) 简单记为 \(W_\ell\) 。

Beam Profile

最简单的情况是 symmetric beam ，也就是 \(\color{black}b(\bm{n}, \bm{n}^\prime)\) 只依赖 \(\color{black}\bm{n}\cdot\bm{n}^\prime\)，此时 \(\color{black}b(\bm{n}, \bm{n}^\prime)\) 可以写成 \(\color{black}b^S(\theta)\)，展开成勒让德级数

\[\color{black}b^S(\theta)=\frac{1}{4\pi}\sum_\ell (2\ell+1)b_\ell P_\ell(\cos\theta)\]

然后利用球谐函数的 addition theorem 和 orthogonality 可以毫不费力地证明

\[\color{black}W_\ell=b_\ell^2\]

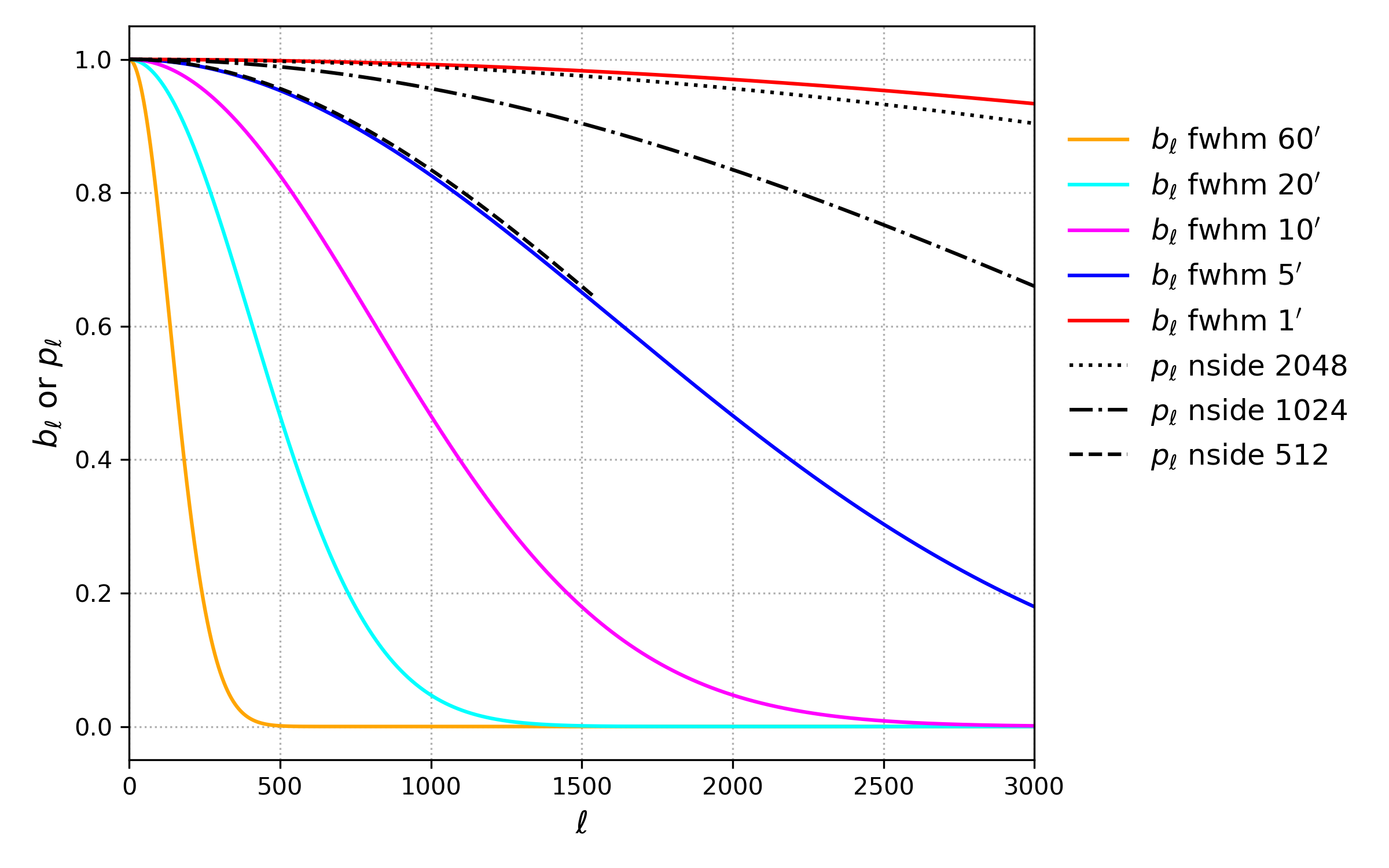
可以用 healpy.beam2cl 把任意的对称的 \(\color{black}b^S(\theta)\) 转换成 \(\color{black}b_\ell\) 函数，beam asymmetry 更加复杂，这里不讨论。

Gaussian Beam Profile

参考 White 1992 文章。一个高斯的 beam 有

\[\color{black}b^S(\theta)=\frac{1}{2\pi\sigma^2}\exp\left[-\frac{\theta^2}{2\sigma^2}\right]\]

一般来说我们有 \(\sigma\ll1\)，利用勒让德多项式的正交性质，可得

\[\color{black}\begin{aligned}b_\ell&=2\pi\int b^S(\theta)P_\ell(\cos\theta)\mathrm{d}\theta \\ &= \frac{1}{\sigma^2}\int_0^\pi \exp\left[-\frac{\theta^2}{2\sigma^2}\right]P_\ell(\cos\theta)\mathrm{d}\theta \\ &= \frac{1}{\sigma^2}\int_0^\infty e^{-x}P_\ell(1-\sigma^2x)\mathrm{d}x\end{aligned}\]

中间做了一个替换 \(x=\theta^2/2\sigma^2\)，积分上限原则上应该使勒让德多项式里的自变量大于负一，这里忽略这一点，因为积分在 \(\theta\) 非常小的时候就已经收敛了，后续贡献的微不足道。上式的积分可以展开为

\[\color{black}\begin{aligned}\int_0^\infty\mathrm{d}x\ e^{-x}P_\ell(1-\sigma^2 x) &= \int_0^\infty\mathrm{d}x\ e^{-x} \sum_{n=0}^\infty \frac{1}{n!}(-\sigma^2x)^nP_\ell^{(n)}(1) \\ &=\sum_{n=0}^\infty\frac{1}{n!}(-\sigma^2)^nP_\ell^{(n)}(1)\int_0^\infty\mathrm{d}x\ e^{-x}x^n \end{aligned}\]

利用

\[\color{black}\int_0^\infty e^{-x}x^n=n!\]

可以得到

\[\color{black}\begin{aligned}\int_0^\infty\mathrm{d}x\ e^{-x}P_\ell(1-\sigma^2 x) &= \sum_{n=0}^\infty(-\sigma^2)^nP_\ell^{(n)}(1) \end{aligned}\]

下面手动求一下 \(P_\ell^{(n)}(1)\)，采用勒让德函数的其中一种表达式

\[\color{black} P_\ell(x)=\sum_{k=0}^\ell\begin{pmatrix}\ell \\ k\end{pmatrix} \begin{pmatrix}\ell+k \\ k\end{pmatrix} \left(\frac{x-1}{2}\right)^k \]

如果对上式求 \(n\) 阶导，并在 \(x=1\) 处取值，那么只会剩下 \(k=n\) 的一项，且当 \(n>\ell\) 的时候，导数为零

\[\color{black}P^{(n)}_\ell(x)=\frac{1}{2^n n!}\frac{(\ell+n)!}{(\ell-n)!} \]

代入上面的积分，得到

\[\color{black}\begin{aligned}\int_0^\infty\mathrm{d}x\ e^{-x}P_\ell(1-\sigma^2 x) &= \sum_{n=0}^\ell(-\sigma^2)^n\frac{1}{2^n n!}\frac{(\ell+n)!}{(\ell-n)!} \end{aligned}\]

有近似（不证明了）

\[\color{black}\frac{(\ell+n)!}{(\ell-n)!}\approx[\ell(\ell+1)]^n\approx\left(\ell+\frac{1}{2}\right)^{2n}\]

这两个近似是同等程度的近似，一般采用第一个近似，最后我们得到

\[\color{black}\begin{aligned}\int_0^\infty\mathrm{d}x\ e^{-x}P_\ell(1-\sigma^2 x) &= \sum_{n=0}^\ell(-\sigma^2)^n\frac{1}{2^n n!}[\ell(\ell+1)]^n\\ &=\exp\left[-\frac{1}{2}\ell(\ell+1)\sigma^2\right] \end{aligned}\]

所以我们得到

\[\color{black}b_\ell=\frac{1}{\sigma^2}\exp\left[-\frac{1}{2}\ell(\ell+1)\sigma^2\right]\]

但通常还存在一个利用 dipole 校准的过程，使得 \(b_{\ell=1}=1\) 所以，最后得到的 Gaussian symmetric beam 的结果是

\[\color{midnightblue}b_\ell=\exp\left[-\frac{\ell(\ell+1)}{2}\sigma^2\right]\]

下面是一个针对自旋的修正

\[\color{midnightblue}b_\ell=\exp\left[-\frac{\ell(\ell+1) - s^2}{2}\sigma^2\right]\]

这个近似在 \(\sigma<0.1\) 的范围内都非常准确，这包括了现在所有的实验的分辨率。可以用 healpy.gauss_beam 获取 Gaussian beam 的 \(b_\ell\) 函数。

Pixel Window Function

参考 HEALPix Primer 的附录。实际上像素化也是一种窗函数，只是这个窗函数是 Top-Hat 的，并不是高斯的，可以用 healpy.pixwin 获取 \(p_\ell\) 函数。