这是偏数学的背景辐射功率谱介绍,参考 Tojeiro 2006 和 Bartlett 2001 文章,最早是 Bond & Efstathiou 1987 这篇文章提出的。
Window Functions in CMB experiments
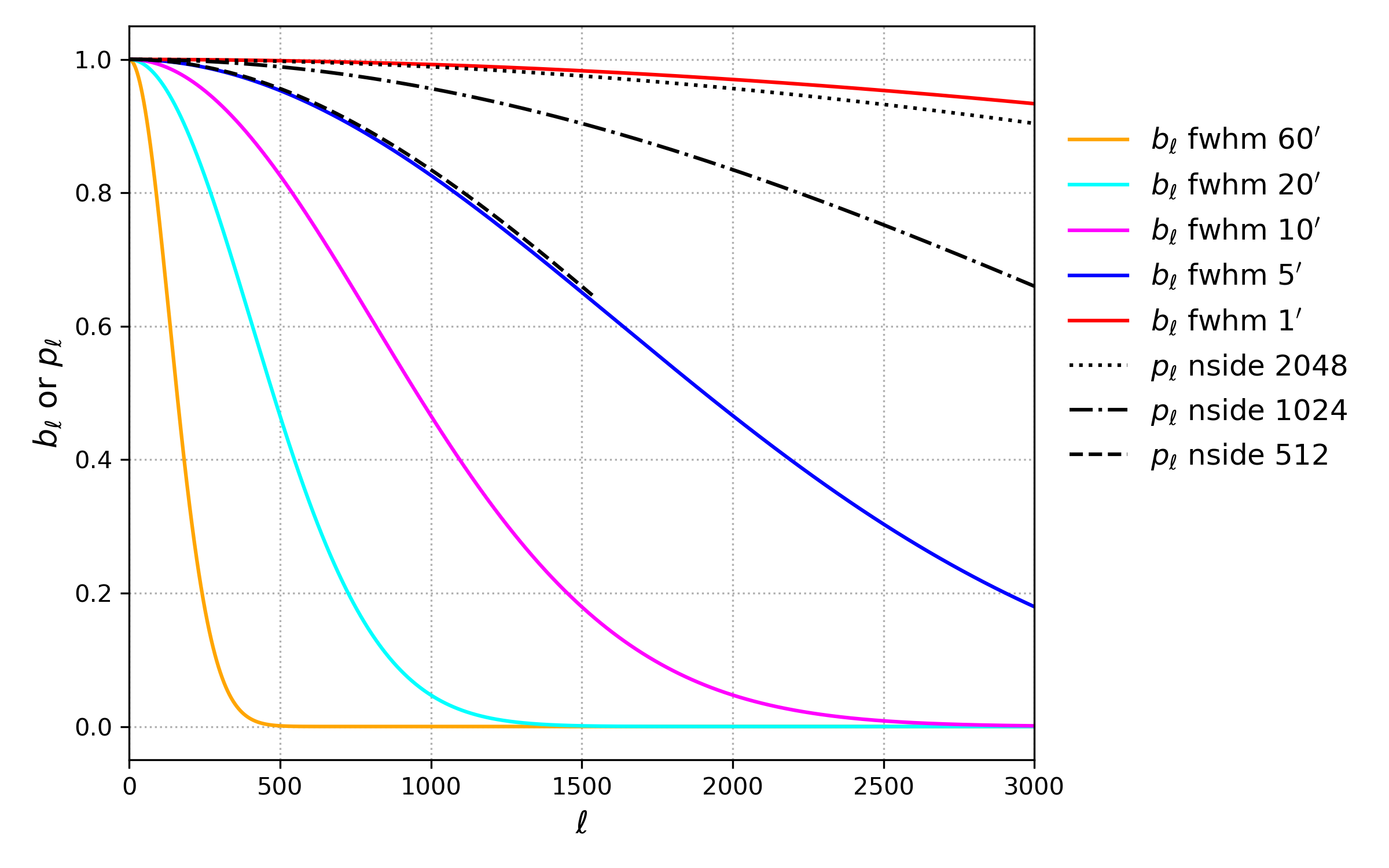
参考 White & Srednicki 1994 和 Page 2003 文章。在微波背景辐射实验中,最重要的一个仪器参数就是仪器分辨率(beam FWHM),它决定了我们是否能够观测到足够小的尺度,这和宇宙参数限制息息相关,同时微波背景辐射透镜效应的重构也依赖小尺度的信号,分辨率足够高,我们的到的重构结果也能够更好。
Spin-weighted Spherical Harmonics
参考 Grant Salton 论文 第二章和 Zaldarriaga & Seljak 1997 的文章。因为斯托克斯参量中的 Q 和 U 场是依赖坐标系定义,普通的球谐变换处理之后的到的物理量也是依赖坐标系的,但是我们需要的物理量最好是不随坐标系变化的,所以需要引入特殊的球谐函数。
在我学习微波背景辐射的早期,为了预防自己不停地温习斯托克斯参量的定义,写了这篇小记。
Definition
参考 Spherical Harmonics USCS Physics 116C Fall 2012 的第一部分来推导拉普拉斯方程在球坐标下的解,并由此引入球谐函数
\[\color{black}Y_{\ell}^{m}(\theta, \phi)=(-1)^{m} \sqrt{\frac{(2 \ell+1)}{4 \pi} \frac{(\ell-m) !}{(\ell+m) !}} P_{\ell}^{m}(\cos \theta) e^{i m \phi} \]
前景最关键的地方在于给不同类型的前景建模,找到和观测最符合的SED(Spectral Energy Distribution),这样才能在多频段观测的 CMB 实验中进行精确的 component seperation 过程。